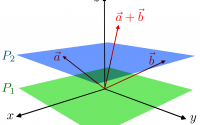
Projective Geometry

As described in last article, projective space can be considered as a tool to mathematically describe the perspective projection. So in this article, we want to go through some basics, but important elements of projective space. After reading this article you will get to understand the followings topics:

Homogeneous coordinates and its properties
Homography matrix
Linear (group) Transformation

Homogeneous Coordinates

As mentioned before, projective space allows to describe the perspective projection using mathematics and homogeneous coordinates is one important element in projective space. It is easy to make homogeneous coordinates of a vector and it will be done just by adding another dimension to it with a value of 1, so to express the vector $v = {\begin{pmatrix} x_1 \ x_2 \ ... \ x_n \end{pmatrix}}^T$ in homogeneous coordinate 1 would be added at the end of the matrix $\tilde{v} = {\begin{pmatrix} x_1 & x_2 & ... & x_n & 1 \end{pmatrix}}^T$ . In projective space just the direction of the vector is important and the length of it is not. Therefore all vectors $pv$ $\forall p\neq0$ are describing the same point in projective space. It means that we can consider any vector $v$ in projective space (n+1 dimensions) and divide it with the last element of the vector to get the homogeneous coordinate:

Any vector in Projective space $\tilde{v}={\begin{pmatrix} x_1 & x_2 & ... & x_n & x_{n+1} \end{pmatrix}}^T$
Homogeneous Coordinates $\tilde{v}={\begin{pmatrix} \frac{x_1}{x_{n+1}} & \frac{x_2}{x_{n+1}} & ... & \frac{x_n}{x_{n+1}} & 1 \end{pmatrix}}^T$
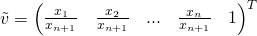
Vector in sub-space affine $v={\begin{pmatrix} \frac{x_1}{x_{n+1}} & \frac{x_2}{x_{n+1}} & ... & \frac{x_n}{x_{n+1}} \end{pmatrix}}^T$

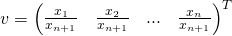
The last element is just a scaling factor and it determines the distance between projection center and projective plane and it can’t be zero because the division by zero is not defined, but in projective space, any point in which the last element is zero will be in a sub-space in infinity. Therefore, as mentioned in Definition of Perspective Projection, Perspective Space & Projective Geometry, projective space is an extension of affine space and it has more points (points at infinity) than affine space.

Homography matrix

The perspective projection can be described by transforming a point in projective space to another point in projective space using a transformation matrix which will be defined as follow:

$\tilde{v}_2 = H \tilde{v}_1$

Where $\tilde{v}_1$ and $\tilde{v}_2$ are points in projective space and the transformation matrix $H$ which is called homography and generally defined as follows:

$H = \left(\begin{array}{rrrr} h_{0,0} & h_{0,1} & \cdots & h_{0,n} \0& h_{1,0} & h_{1,1} & \cdots & h_{1,n} \0& \vdots & \vdots & \ddots & \vdots \0& h_{n,0} & h_{n,1} & \cdots & h_{n,n}\end{array}\right)$

An important property of this matrix is that it is full rank, which means, there is no linear relation between each row vector.

Linear Transformation

By considering transformation between two points in projective space as a linear transformation using homography matrix (The linearity depends on the elements/form of the transformation matrix), then by multiplying two (or more) linear transformation matrix, we can achieve a new linear transformation matrix:

$H_3 = H_1H_2$

By this definition, we can now reduce the computation time and process by first multiplying two or more transformation matrix to get a new transformation matrix and then apply it to the image.

Summary

So far we got familiar with homogeneous coordinate, homography matrix and linear transformation. These basics are important to know if you even just want to do image processing. In the next article, I will mention some other properties in projective geometry and then we will continue with low-, mid- and high- level vision.

Continue Reading: Summary of Projective Geometry

Last post: Definition of Perspective Projection, Perspective Space & Projective Geometry