Local Feature and Harris Corner Detection
In the last three posts, we have learned some important basics in computer vision and in this post, I want to talk about the concept “Feature” which plays an important role in different levels of image processing.
Feature (local Feature)
In image processing, feature (local feature) is basically a piece of image (patch) which can be used for doing some tasks, for instance, stitching two image to create a panorama is a task (we will continue with this example for the rest of the post) and to do that we can find some features which exist in both images and then put the images on each other to create the panorama (of course we should consider some transformations too). Local features are corners, edges, blobs. Basically, it does not matter what a feature represents, it is important that the feature is distinguished from its neighbors/surroundings. So, generally, depending on applications, what we will do is finding patches in an image that are useful or have some meaning for accomplishing a task. But why local features are good/useful? Generally, local features will give us some advantages:
- Quantity, a large number of them can be found in an image.
- Locality which means features are robust to occlusion and clutter.
- Distinctiveness, it is possible to differentiate them in a large database of features.
- Efficiency, they are small patches and so it is possible to work with them in real-time.
Along with all the above advantages which local features give, uniqueness is a key point for a good feature which introduces two advantages:
- feature can be found easily
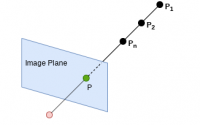
- It is not mistaken for different features. For instance, if we want to find out how close are two patches, we will calculate the Sum Squared Difference (Residual sum of squares) between two patches (images
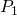 ,
, 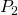 ) using
) using 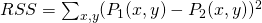 and if the difference is not much it means the images are close to each other.
and if the difference is not much it means the images are close to each other.
To recap, features could be anything edges, corners, etc. but it should be unique so it would be easier to find it in other patches. Also, they should be invariant to transformations which means they should be geometric invariance (translation, rotation, and scale) as well as photometric invariance (brightness, exposure, etc.). Generally, corners are good features but edges can be invariant to brightness but not to other transformations. Btw., we will talk about geometric transformations next article.
Harris Corner Detector
Corners are basically good features in an image and somehow unique, but how do we find unique patches and corners in an image? The simple way for detecting a unique feature is finding all the patches (features) in an image and calculate the distance function between all patches in the same image if the difference is too much, hopefully, this patch can be considered as a unique patch for this image. Then, in case of a panorama, we calculate the distance between the unique patch in one image and all patches in another image, and if the distance is not much we consider them as the same patch and then the two images can be stitched together. The better way would be defining a measure for patches and compare them with each other to find the unique patch, so instead of calculating the difference between all patches what we can do is basically calculate the self-difference for each patch which is auto-correlation:
![]()
in which ![]() is a weight and
is a weight and ![]() is the pixel and
is the pixel and ![]() is the shift value. If the result of Autocorrelation is too much, then it can be a good measure for considering the patch a good patch. Generally, corners are good because they produce high self-difference whereas edges don’t produce high difference by just shifting. So the patches which have strong gradients in more than one direction are good (corner). But the problem with these two ways is that they need lots of computational resources, although autocorrelation is faster. So we need to approximate the self-difference which can be done through
is the shift value. If the result of Autocorrelation is too much, then it can be a good measure for considering the patch a good patch. Generally, corners are good because they produce high self-difference whereas edges don’t produce high difference by just shifting. So the patches which have strong gradients in more than one direction are good (corner). But the problem with these two ways is that they need lots of computational resources, although autocorrelation is faster. So we need to approximate the self-difference which can be done through structure matrix. Structure matrix is the weighted sum of nearby gradient information:
![]()
where r defines a region around the pixel p and w(r) is a weight for this region and ![]() is the gradient of the image in the x-direction. please note that we should calculate this matrix for each pixel. The eigenvectors and value of structure matrix summarize the distribution of the gradient information of nearby pixels (area
is the gradient of the image in the x-direction. please note that we should calculate this matrix for each pixel. The eigenvectors and value of structure matrix summarize the distribution of the gradient information of nearby pixels (area r) which means eigenvector will give us the direction and eigenvalue the value of gradient in r (how much varies in the pixel value in the gradient direction). We have talked about the gaussian and gradient in the last two posts so it is basically “straight forward” to calculate structure matrix in two steps:
- calculate the gradient of the entire image in both directions. So it will need two arrays for storing the gradient in x and y directions and array for multiplication of both gradients.
- get the Gaussian smoothing of this gradient information (these three matrices) and so what we end up doing is just a weighted sum of nearby gradients with each other.
Just to remind you, eigenvector and eigenvalue of matrix A will be defined as follow:
![]()
Where ![]() is the eigenvector of A and
is the eigenvector of A and ![]() is the eigenvalue of A. And trace of a matrix is the sum of elements on the main diagonal of a square matrix (
is the eigenvalue of A. And trace of a matrix is the sum of elements on the main diagonal of a square matrix (![]() ).
).
What we want are patches where eigenvalues are both large (this is a 2×2 matrix and has two eigenvalues and two eigenvectors and one of them is always going to be smaller than the other one) and it is probably some sort of corner, but if we have two eigenvalues of the structure matrix which are very small then we know there is not really any gradients in any of surrounding pixels. So:
- if
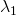 and
and 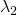 are both small, then there would be no gradient in the patch
are both small, then there would be no gradient in the patch - if
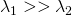 (one of them is much bigger than the other one), then there is a gradient in one direction and it is probably an edge
(one of them is much bigger than the other one), then there is a gradient in one direction and it is probably an edge - if both are big and similar, then there would be gradient directions and it is probably a corner
Calculating eigenvalues for every pixel in the image need computational resources, so we should estimate that. For that there are different algorithms, for instance by using determinant (![]() ) and trace (
) and trace (![]() ) of structure matrix we can estimate
) of structure matrix we can estimate ![]() :
:
-
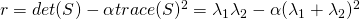 where
where 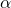 is an small number between 0.04 and 0.06. If r is a negative number then this patch is an edge and if r >> 0 then there is a corner in that patch.
is an small number between 0.04 and 0.06. If r is a negative number then this patch is an edge and if r >> 0 then there is a corner in that patch. -
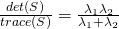
what we are basically looking for places in the image where the second eigenvalue is large (![]() ), so these places have gradients in different directions and are areas with high self-difference (low self-similarity).
), so these places have gradients in different directions and are areas with high self-difference (low self-similarity).
After calculating the structure matrix we can basically use non-maximum suppression to reduce the number of detected patches. The whole process is called Harris Corner detection.
Descriptor
For finding the matches between the patches of different images, we use descriptors. What descriptors do is basically describing the elementary characteristics of each patch such as shape, color, texture or motion, etc. In case of a panorama, for finding the matches between the patches of the images we will calculate the distance metrics or RSS (![]() ) for descriptors and if the result is low, so probably the selected patches are the same.
) for descriptors and if the result is low, so probably the selected patches are the same.
Summary
As we know good features are unique and also they should be invariant to geometric and photometric parameters of an image. Corners are basically very good features because they provide some invariance to geometric (rotation invariant) and photometric (somehow illumination invariant) but they are not scale-invariant. The method used for corner detection called Harris Corner detection which will be done in the following steps:
- Calculate the derivative of the image (I) in both x and y directions (
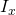 and
and 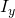 )
) - Calculate three measures for structure matrix (
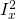 ,
, 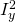 and
and 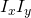 )
) - Calculate the gaussian of the area around the selected pixel (the weighted sum)
- Estimate response based on the smallest eigenvalue
- Non-max suppression to realize useful corners